Asymmetric Steel Rolling Process: Part Two
Abstract
Asymmetric steel rolling is a key technique to help minimize defects that can occur in the rolling process because of process variations such as uneven heating of the strip or imprecise elements of rolling mill itself.
This paper will cover a range of experimental conclusions from in depth analysis of the process including specific observations about the resulting material stability and its impact on its relevant physical properties.
In recent years, rolling with imposed asymmetry has gathered interest to introduce a through thickness shear texture effect in a rolled sheet. It has been also considered that imposing asymmetric conditions just by varying the rolling parameters in conventional rolling is the most efficient way to introduce shear into the sheet. Several studies report that the added shear strain in rolling can lead to increased grain refinement, tensile strength improvement, and tilt/rotation of the rolling texture, so one can tailor the deformation texture anisotropy.
Based on the type of applied asymmetry, different nomenclatures have been given to asymmetric rolling processes. There are three ways to introduce asymmetry: difference in roll diameter, in angular speed, or in friction. However, the pre-notion was that the effect of these different ways of imposed asymmetry in rolling remains mostly similar on deformed texture and microstructure, except the tribological type of asymmetry, which is reported to be much less effective than the others.
The aims of the Satyaveer Singh Dhinwal et al was to reveal texture evolutions as a function of thickness reduction per pass. Single pass asymmetric rolling was carried out on extra low carbon steel. The effect of texture rotation was also examined in terms of microstructure evolution.
A schematic of the experimental setup is presented in Figure 1, showing the positions of the neutral points and the reference system.
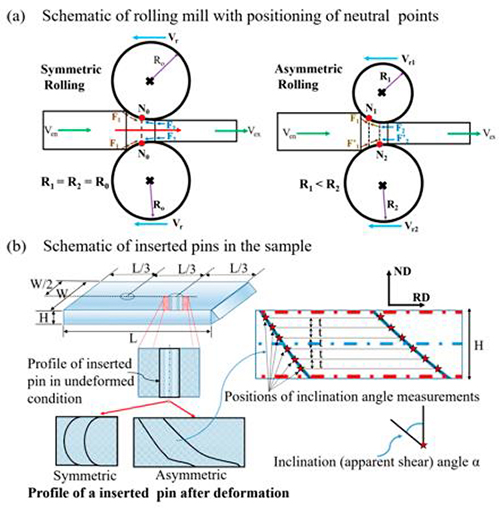
Figure 1: Schematic of the experimental setup, representing positons of (a) neutral points and (b) inserted pins in a sample.
On the basis of the experimental results, they draw the following conclusions:
1. The rolling texture approaches the shear texture when the applied thickness reduction per pass is 50% or above, together with an asymmetry ratio of 1:2.
2. The value of the shear coefficient is independent of the applied number of passes but sensitive to its measurement position along the thickness of the sheet. This measured value in a given pass with inserted new pin can be related to the expected rotation of the texture to be achieved in asymmetric rolling.
3. Under effective asymmetric conditions, there is more grain fragmentation in the mid thickness area of a sheet due to the increased lattice rotation inherent in shear compared to the symmetric case.
4. Both average grain size and JMAK exponent remain smaller in the case of asymmetric rolling than for symmetric rolling after recrystallization.
5. Avery different recrystallization texture forms in optimal asymmetric rolling conditions compared to the conventional recrystallization textures observed in symmetric rolling.
In the work of Laszlo S. Toth et al, asymmetric rolling of IF steel is studied in comparison with conventional rolling. The objective is to examine the characteristics of the ideal crystal orientations together with the variations in the texture during asymmetric rolling ASR. As the ideal orientations for ASR have not been identified yet, first a theoretical study was carried out using an orientation stability analysis.
The present analysis is based on an earlier work of Toth et al. (1990) carried out for ferrite textures in symmetric rolling SR which was recently generalized by Toth (2008) for textures in other materials during plastic deformation in different modes. As an application, the ideal ND fibre was selected in this work to study the effects of ASR on the development of the texture. R values were also calculated using the viscoplastic self-consistent polycrystal model (VPSC) and were compared to measured values.
From the present investigation, the following major conclusions can be drawn:
(1) A stability analysis carried out for asymmetric rolling in Euler space. It has been found that due to the shear component in ASR, the ND fibre is displaced in orientation space. This displacement is in the opposite direction when the shear component is reversed.
(2) Polycrystal simulations showed that the ND fibre can be maintained during ASR up to about a shear of γ = 2 during a rolling strain of ε = 1 when the VPSC model is used.
(3) Starting with an ideal ND fibre, the predicted R values in ASR are almost as high as for symmetric rolling if the shear component is not too high. An optimum value of γ = ±1 has been identified for ε = 1 rolling strain; below this limit, the R value decreases drastically.
(4) It was shown by simulations, that cyclic asymmetrical rolling (ASRr) leads to better R values than SR. Experimental work on IF steel confirmed this main finding.
Czytaj więcej
Znajdź natychmiast tysiące obrazów mikrostruktur!
Total Materia Horizon zawiera unikalną kolekcję obrazów mikrostuktur obejmujących szeroki zakres stopów metali, krajów, norm i obróbek cieplnych.
Uzyskaj BEZPŁATNE konto testowe w Total Materia Horizon i dołącz do społeczności ponad 500 000 użytkowników z ponad 120 krajów.