Reoxidation of Steels
Abstract
The internal cleanliness of steel is determined by the composition, size, number and distribution of its inclusions. It should be strictly controlled to ensure the castability of the liquid steel as well as the functional properties of the final product. The inclusions are formed during converter tap, ladle treatment and continuous casting of the steel and they can be oxides, sulfides and nitrides.
The oxides are formed by the reaction of dissolved reactive metals and oxygen, either dissolved in the steel or originating from the atmosphere, refractories or slags. Erosion of the refractories and slag dispersion can also be sources of new inclusions.
Introduction
The internal cleanliness of steel is determined by the composition, size, number and distribution of its inclusions. It should be strictly controlled to ensure the castability of the liquid steel as well as the functional properties of the final product. The inclusions are formed during converter tap, ladle treatment and continuous casting of the steel and they can be oxides, sulfides and nitrides. The oxides are formed by the reaction of dissolved reactive metals and oxygen, either dissolved in the steel or originating from the atmosphere, refractories or slags. Erosion of the refractories and slag dispersion can also be sources of new inclusions.
Most of the oxide inclusions are formed during deoxidation and subsequent reoxidation processes. Liquid steel processing includes measures that remove the inclusions to the slag, such as argon stirring of the ladle and flow pattern control in tundish. Therefore, the composition of the ladle, the tundish and the mould slags should be optimized to pick up and dissolve inclusions, although a compromise with the other functions of the slag is necessary. The formation of new oxides is to be avoided because entrainment of these particles by the steel deteriorates internal cleanliness. The steel is therefore protected from reoxidation as adequately as possible, e.g. by shrouding the steel stream from ladle to tundish and tundish to mould using nozzles, by using stable refractory materials and by utilizing slags low in FeO+MnO content.
In ladle refining processes, (FetO + MnO) content in slag should be lowered less than 1 wt% for the effective desulphurization and the suppression of the steel reoxidation. This brings about an increase in production cost and processing time because of the excessive injection of raw materials. Decreasing the activity coefficients of FetO and MnO is an alternative solution for controlling the activities of the reducible oxides while maintaining high (FetO + MnO) content.
As an illustration of the reoxidation of steel by adding the usual deoxidizers (Si and Al) are showed in this article.
Reoxidation of Steel By Adding Silicon
Silicon is a strong deoxidizer. If [%Si] ≥ 0.2, [%C] ≤0.15, and the temperature of the melt is 1873 K, then the following reaction is possible:
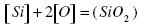 .......... (1)
.......... (1)
The equilibrium constant of the reaction (1) is
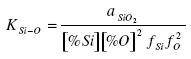 .......... (2)
.......... (2)
If the standard state is solid silica, then in the thermodynamic calculation of deoxidation of steel by silicon aSiO2 is taken as being equal to one. According to Kramarov if the slag is saturated with silica then:
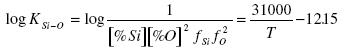 .......... (3)
.......... (3)
So the deoxidation ability of silicon depends on its concentration and the temperature of the metal, but also on the activity aSiO2. At high temperature and the some value of [%Si], [%Mn] and [%C], its deoxidation ability is something smaller than that of carbon, but considerably higher than manganese.
At some point during the increase in the concentration of silicon in the Fe-Si melt the minimum concentration of oxygen [%O]min is obtained; any further increase in [%Si] results in an increase of [%O]. At first sight this suggests that the product of the activity coefficients (foSi)2 fSiSi decrease faster than the increase of [%Si]. In agreement with the expression for the equilibrium constant (2), the extreme value for the concentration of silicon [%Si]extr. corresponds to the minimum concentration of [%O]min.
When calculating the critical value of [%O]min. and [%Si]extr., it is necessary to express equation (2) in the following way
ln[%O] = ½ ln aSiO2 - ½ ln KSi-O - ½ ln [%Si] - ½ ln fSiSi - ln fOSi .......... (4)
The logarithms of the coefficients of activity are:
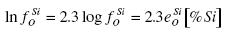 .......... (5)
.......... (5)
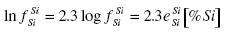 .......... (6)
.......... (6)
and the interaction parameters are eOSi = -0.133 and eSiSi = 0.098. The interaction parameters eO0 and eSi0 are neglected because the concentration of oxygen is relatively small (log fOO ≈ 0, log fSiO = eSiO [%O] ≈ 0, and follows fOO ≈ 1 and fSiO ≈ 1), and the activity aSiO2 = 1.
To obtain [%Si]extr, it is necessary to take the first derivative of the concentration of oxygen divided by the concentration of silicon and set the equation equal to zero under specific conditions:
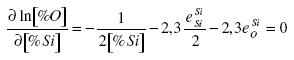 .......... (7)
.......... (7)
The second derivative is greater than zero:
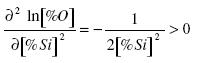 .......... (8)
.......... (8)
Consequently, the function has a minimum. The concentration of silicon at which [%O] is a minimum:
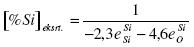 .......... (9)
.......... (9)
On the basis of the quote d value of the interaction parameters for T=1873 K and aSiO2=1 [%Si]extr. a value of 2.59% is obtained. In that case fSiSi = 1.794 and fOSi = 0.452. For steel melts there is also the influence of the other elements on fSi and fO. At 1873 K the equilibrium constant KSi-O = 25099. The minimum concentration of oxygen in the melt is:
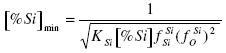 .......... (10)
.......... (10)
By inserting reasonable values into equation (10) a minimum concentration of oxygen [%O]min = 6.5 x 10-3 % is obtained.
Reoxidation of Steel By Adding Aluminum
The deoxidation of steel by aluminum proceeds according to there action:
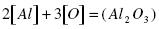 .......... (11)
.......... (11)
The equilibrium constant may be determined from:
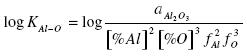 .......... (12)
.......... (12)
At 1873 K, the equilibrium constant is KAl-O = 4.9 x 1013. In the calculation it is assumed that aAl2O3 = 1, because at small values of [%Al] (0.001-0.01) the equilibrium concentration (%FeO) in the slag is neglected, so the products of deoxidation are solid Al2O3 or an oxide phase saturated with alumina.
The coefficient of activity of aluminum fAl = fAlAl fAlO = O ≈ 1, and the coefficient of oxygen fO = fOO fOAl = ≈ fOAl, which is an approximation, because the influence of the other elements present on fO is very strong, and fO is <1. The equilibrium concentration of oxygen in the melt may be expressed with:
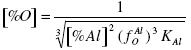 .......... (13)
.......... (13)
An analysis of the equation (13) shows that at some increment of the concentration of aluminum the activity factor fOAl decreases faster than [%Al]2/3 increases. The result is that at some value of [%Al] the [%O]min. is obtained. A further increase in [%Al] results in an increase of [%O]. To obtain [%Al]extr., the first derivative of the logarithm of the concentration of oxygen divided by the concentration of aluminum must be set equal to zero:
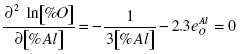 .......... (14)
.......... (14)
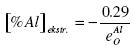 .......... (15)
.......... (15)
According to Kulikov, interaction parameter e0Al = -1.17, which corresponds to [%Al]extr. = 0.248. According to formula (13) the minimum concentration of oxygen [%O]min = 1.35 x 10-4 % is obtained.
Access Precise Properties of Structural Steels Now!
Total Materia Horizon contains property information for 150,000+ structural steels: composition, mechanical and physical properties, nonlinear properties and much more.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.