Control of Sulfur in Melts
Abstract
Sulfur has a strong surface activity both in binary (Fe-S) and ternary (Fe-C-S, Fe-Si-S) alloys. It has been concluded from the results of numerous studies that sulfur can exist in two forms in molten iron: in one case it forms an interstitial solutions, and in other partially substitutional solutions. It has been found that the activity of sulfur increase substantially when carbon and silicon are present in the melt. This explains why pig iron can be desulfurized more readily than steel.
Sulfur (S) is a typical metalloid. The radius of sulfur atom is 1.05 Å. It easily acquires two electrons to form an ion S2-. The coefficient of diffusion of sulfur in liquid iron is 0.74x10-4, 13x10-4, 1.9x10-5 cm/s, according to various experimental data. Sulfur has a strong surface activity both in binary (Fe-S) and ternary (Fe-C-S, Fe-Si-S) alloys. It has been concluded from the results of numerous studies that sulfur can exist in two forms in molten iron: in one case it forms an interstitial solution, and in other partially substitutional solutions. It has been found that the activity of sulfur increase substantially when carbon and silicon are present in the melt. This explains why pig iron can be desulfurized more readily than steel.
A good understanding of the desulphurization of hot metal and liquid steel has been developed in terms of slag-metal reactions, based on a number of studies of the partition of sulfur between liquid slag and liquid iron. These results show that a highly basic slag, high temperature and reducing conditions enhance desulphurization via slag-metal reactions.
Sulfur Equilibrium between Liquid Iron and Slag
The desulphurization of liquid iron with slag may be examined on the basis of the following reaction (1), in which the equilibrium constant can be expressed by equation (2).
[S] + (O2-) = (S2-) + [O] .......... (1)
log K1 = as2-. ao / as. ao2- .......... (2)
where,
- ao, as: the activities of oxygen and sulfur in liquid iron, respectively
- ao2-, as2-: the activities of oxygen and sulfur ions in slag, respectively.
The sulfur partition ratio between metal and slag is given by equation (3) according to reaction (1).
LS = (wt%S) / [wt%S] = K1 • ao2- • fs / ao • fs2- .......... (3)
where,
- fs, fs2- : the activity coefficients of sulfur in liquid iron and slag, respectively.
Since the values of K1, ao2- and fs2- cannot be determined experimentally, the sulfide capacity is defined as equation (5) on the basis of reaction (4) and is utilized for the examination of desulphurization in iron and steel making processes.
½ S2 + (O2-) = (S2-) + ½ O2 .......... (4)
CS = (wt%S) • (PO2 / Ps)½ = K4 ao2- / fs2- .......... (5)
where,
- PO2 and Ps are the oxygen and sulfur partial pressure in atm;
- K4 the equilibrium constant of reaction (4).
In order to calculate the value of CS, the equilibrium constants of reactions (6) and (7) are substituted into equation (5), and equation (8) is obtained.
½ O2 = [O] .......... (6)
½ S2 = [S] .......... (7)
log Cs = log (wt % S) ao / as + 936 / T-1.375 .......... (8)
By the use of the interaction coefficients of sulfur and oxygen in liquid iron, the values of CS can be calculated from equation (8).
As an illustration, the calculation of sulfide capacity (CS) has been given for CaO-MgO-Al2O3-SiO2 ladle slags.
In order to examine the relationship between CS and composition of slag, the following relationship is assumed to hold at certain temperatures.
log CS = α (NCaO + KMgO • NMgO + KAl2O3• NAl2O3 + KSiO2 • NSiO2)+ β .......... (9)
where:
- α, β: the constants
- Ni, Ki: the mole fraction and the lime equivalent coefficient of i-component in the slag phase, respectively.
At 1600°C, the values of KMgO, KAl2O3 and KSiO2 determined by trial and error are 0.1, -0.8 and -1.0, respectively. As shown in Figure 1, there are linear relations between log Cs and (NCaO + 0.1 NMgO – 0.8 NAl2O3 – NSiO2) at 1575, 1600 and 1650°C.
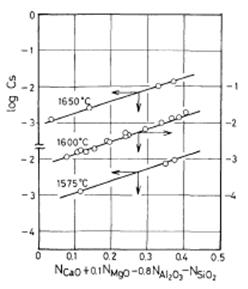
Figure 1: Plot of the log Cs against NCaO + 0.1NMgO – 0.8NAl2O3 – NSiO2 at 1575, 1600 and 1650°C
The three lines obtained by the method of least squares are shown in the figure. The intercepts of the lines were determined by the use of the slope at 1600°C because the most runs were done at this temperature. The following equation was obtained as a function of temperature.
log CS = 3.44 (NCaO +0.1NMgO – 0.8NAl2O3 – NSiO2) - 9894 / T+2.05 .......... (10)
The observed values of log CS with the correlation coefficient (R) of 0.99 and the standard deviation (σ) of 0.044 can well be expressed by the above equation.
On the other hand, log LS may be expressed by the following general equation derived from equations. (3), (8) and (10).
log LS = α ∑ Ki•Ni - log [wt%O] - β .......... (11)
where,
- ∑ Ki•Ni = NCaO +0.1NMgO – 0.8NAl2O3 – NSiO2.
The experimental data were arranged by the method of least squares according to equation (11) and the following relationship was obtained.
log LS = 3.44 ∑ Ki•Ni - log [wt% O] - 10 980 / T+3.50 .......... (12)
Relationship Between Sulfide Capacity and Theoretical Optical Basicity
Duffy and Ingram defined the theoretical optical basicity (Λ) as follows:
Λ = ∑ (xi / fi) .......... (13)
where, xi, fi : the equivalent cationic fraction and the basicity moderating parameter for the constituent cation i, respectively.
It was verified by them that fi can be expressed by the Pauling's electronegativity xi as follows:
fi =1.36 (xi -0.26) .......... (14)
It was also found by Duffy and Ingram that log CS are linearly correlated to the theoretical optical basicity.
As an illustration of the above mentioned the experimental results performed on ladle CaO-MgO-Al2O3-SiO2 slags has been given. The values of log CS are plotted against the optical basicities at 1575, 1600 and 1650°C, as shown in Figure 2.
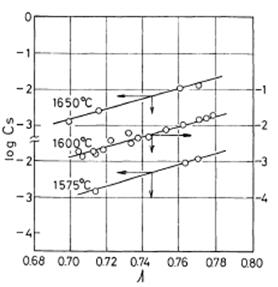
Figure 2: Plot of log CS against theoretical optical basicity Λ
The slopes and intercepts of the lines were determined by the method of least squares, and the following linear relationship was obtained as a function of temperature.
log CS = 14.20Λ - 9 894 / T -7.55 .......... (15)
As described above, it can be seen that both the sum of lime equivalent and the optical basicity are able to be used as parameters for the representation of sulfide capacity. From the relationship between these two parameters, the linear equation (16) from regression was obtained.
Λ = 0.24(NCaO + 0.1NMgO – 0.8NAl2O3 – NSiO2) + 0.67 .......... (16)
The correlation coefficient (R) is larger than 0.99, and the standard deviation (σ) is smaller than 0.01. This shows that the two parameters have almost the same character for the representation of sulfide capacity of slag.
Equilibrium of Oxygen Partition between Metal and Slag
It is well known that the oxygen potential exerts a large influence on the sulfur partition between metal and slag. The equilibrium of reaction (17) was determined by the use of the value of the equilibrium constant (18) reported in literature.
(FeO) = [Fe] + [O] .......... (17)
log K17 = log ao / aFeO = -6 150 / T + 2.604 .......... (18)
Equation (18) may be modified to the following equation.
log [wt%O] = log NFeO + log γFeO - log fo - 6 150 / T + 2.604 .......... (19)
where γFeO is the activity coefficient of FeO on the basis of mole fraction.
Since log γFeO is a function of temperature and slag composition, log [wt%O] can be expressed by an equation including the term of log NFeO, then the following relationship was obtained.
log [wt%O] = 0.905 log NFeO -0.15 ∑ Ki•Ni - 6 340 / T + 3.115 .......... (20)
where, ∑ Ki•Ni = NCaO + 0.1NMgO – 0.8NAl2O3 – NSiO2.
As shown in Figure 3, the observed values of log [wt% O] agree well with the values calculated from the equation (20). By substituting equation (20) into equation (12), equation (21) is derived:
log LS = 3.59 ∑ Ki•Ni -0.905 log NFeO – 4 640 / T + 0.385 .......... (21)
The above equation can conveniently be used for the estimation of the sulfur partition between liquid iron and slag in which the oxygen content in liquid iron is not analyzed. Next, the values of γFeO calculated from the equation (19) were arranged by the way similar to that described previously, and the following relationship was obtained.
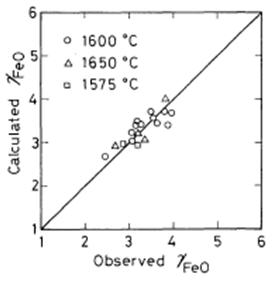
Figure 3: Comparison of the observed log [wt%O] with calculated log [wt%O] from the equation (20)
Find Instantly Precise Compositions of Materials!
Total Materia Horizon contains chemical compositions of hundreds of thousands materials and substances, as well as their mechanical and physical properties and much more.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.