Engineering Stress-strain Curve: Part Two
Abstract
This article examines the fundamental concepts of engineering stress-strain curves and their significance in materials testing. It explores the relationship between stress and strain in engineering materials, explaining key parameters including tensile strength, yield strength, and elastic modulus. The discussion encompasses the distinct differences between true stress-strain and engineering stress-strain curves, their interpretations, and practical applications in materials science and engineering design. Understanding these relationships is crucial for material selection and structural design in engineering applications.
Introduction to Stress-strain Analysis
The engineering tension test serves as a cornerstone in materials science, providing essential design information and material specifications. During testing, specimens undergo controlled uniaxial tensile force application while elongation measurements are recorded. The resulting stress-strain relationships reveal critical material properties used in engineering design and quality control.
Factors Affecting Stress-strain Behavior
Multiple factors influence a metal's stress-strain curve characteristics, including:
- Material composition
- Heat treatment history
- Previous plastic deformation
- Strain rate
- Temperature
- Testing conditions
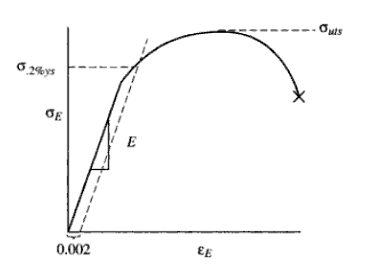
Figure 1: Engineering stress-strain curve for a typical engineering alloy
Key Properties and Measurements
The stress-strain curve reveals several crucial material properties:
Elastic Modulus (Young's Modulus)
The elastic modulus (E) represents the slope of the initial linear portion of the stress-strain curve, defined by the relationship σ = Eε. This property indicates material stiffness during elastic deformation.
Yield Strength
The 0.2% offset yield strength (σ0.2%YS) marks the transition from elastic to plastic deformation. This value is determined by intersecting a line parallel to the elastic portion, offset by a strain of 0.002.
Ultimate Tensile Strength
The ultimate tensile strength (σuts) represents the maximum stress value on the engineering stress-strain curve, indicating the highest load capacity before necking occurs.
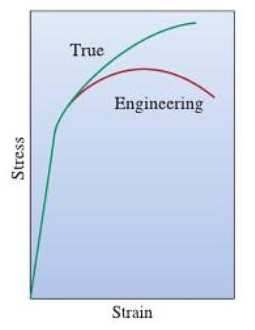
Figure 2: Comparison of engineering and true stress-strain curves
Engineering vs. True Stress-strain Curves
A fundamental distinction exists between engineering and true stress-strain curves. Engineering stress calculations use the original cross-sectional area, while true stress considers the instantaneous area during deformation. This difference becomes particularly significant during plastic deformation, where true stress continues to rise while engineering stress reaches a maximum before declining.
Conclusion
Understanding the nuances between engineering and true stress-strain relationships is crucial for accurate material characterization and engineering design. The engineering stress-strain curve, while simplified, provides valuable information about material behavior under load and serves as a fundamental tool in materials engineering.
Access Thousands of Stress-Strain Diagrams Now!
Total Materia Horizon includes a unique collection of stress-strain curves of metallic and nonmetallic materials. Both true and engineering stress curves are given, for various strain rates, heat treatments and working temperatures where applicable.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.