Cleavage Fracture Toughness
Abstract
Understanding material fracture toughness is a key part of the development of the preventative measures which should be identified to help prevent brittle fracture in a range of applications.
Various experimental and theoretical studies, including specific stress models, show that although the process is understood, more advanced quantitative methods should be used to help drive improvement of knowledge in this area.
The brittle-to-ductile transition (BDT) in Body Centered Cubic (BCC) metals and alloys is of both technological and scientific importance. In order to prevent brittle fracture in steel structures such as large ships and offshore structures, it is critically important to predict fracture toughness by clarification of the crack initiation mechanism. It is widely known that fracture appearance transition temperature of Charpy impact testing is linearly changed with the reciprocal of the square root of grain size.
The reason is, however, not clarified completely. It is also known that the fracture toughness depends on the size of the brittle phase such as cementite. In addition, several formulations to evaluate the influence of microstructures including the size of ferrite grain and brittle phase are proposed by Almond et al. (1969), Petch (1986) and Bingley (2001).
Although these proposals are significant the problem of improved accuracy still remains. The cleavage fracture of steel is generally interpreted by the weakest link mechanism which is differentiated from yielding and work hardening. The scatter in the fracture toughness is therefore its most essential property. This is a principal reason of the difficulty to quantify the influence of microstructures on fracture toughness.
It is generally accepted that the transgranular cleavage fracture of steels in the transition temperature range is governed by the propagation of micro-crack nucleated at carbide particles, non-metallic inclusions and martensitic islands. McMahon and Cohen had first demonstrated that the cracking of carbide particles at ferrite grain boundaries represents a primary cleavage fracture mechanism in steels.
Many authors demonstrated up to the present day that brittle cleavage fracture in steels initiates at some particles that are harder and more brittle than the surrounding ferrite matrix. The cleavage fracture is promoted by factors that produce locally elevated tensile stress, since tensile stress governs the propagation of a micro-crack as a Griffith crack.
The cleavage crack once initiated can propagate with low energy dispersion and results in unstable propagation. It implies that the fracture obeys the Weakest Link Analogy and statistical distribution of the critical fracture stress shows the Weibull distribution. Formulation of the Weibull stress criterion to describe the cleavage fracture of steels was first performed by Beremin and Mudry.
The cleavage fracture toughness of steels is quite sensitive to metallurgical factors, and it strongly depends on temperature, strain rate and constraint due to variation in the specimen thickness, in the notch depth and in the scale of yielding at the crack tip. Degradation in the toughness due to pre-straining, irradiation and strain aging, has been often reported. However, the factors that deteriorate the toughness have not been individually and experimentally discussed in recent times. The dislocation theory and other microscopic approaches may significantly contribute for analysis on the fracture and toughness of steels, while they give little quantitative information on mechanical factors responsible to the toughness.
On the other hand, the mezzoscopic description or formulation of the toughness can be expected to give more comprehensive, and a more quantitative understanding of all subjects responsible for the toughness, and it may lead to the development of the general improvement of material toughness.
The Weibull Stress Model
The Beremin model adopts a two-parameter Weibull distribution to describe the cumulative failure probability
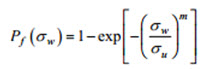 .... (1)
.... (1)Here σw represents the Weibull stress defined as the integral of a weighted value of the maximum principal (tensile) stress (σ) over the process zone of cleavage fracture (i.e., the crack front plastic zone).
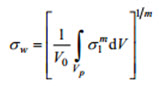 .... (2)
.... (2)In Equation (2), Vp represents the volume of the cleavage fracture process zone, V0 is a reference volume and m denotes the Weibull modulus which defines the shape of the probability density function for microcrack size in the fracture process zone.
Previous studies, e.g., Beremin, show that the probability density function for microcracks having size a has the form f (a) = c where c is a constant and γ defines the shape of the microcrack distribution. The relationship between m and γ follows m = 2γ − 2. In Equation (1), σu represents the scale parameter of the Weibull distribution and defines the microscale material toughness when the cumulative failure probability is 63.2%.
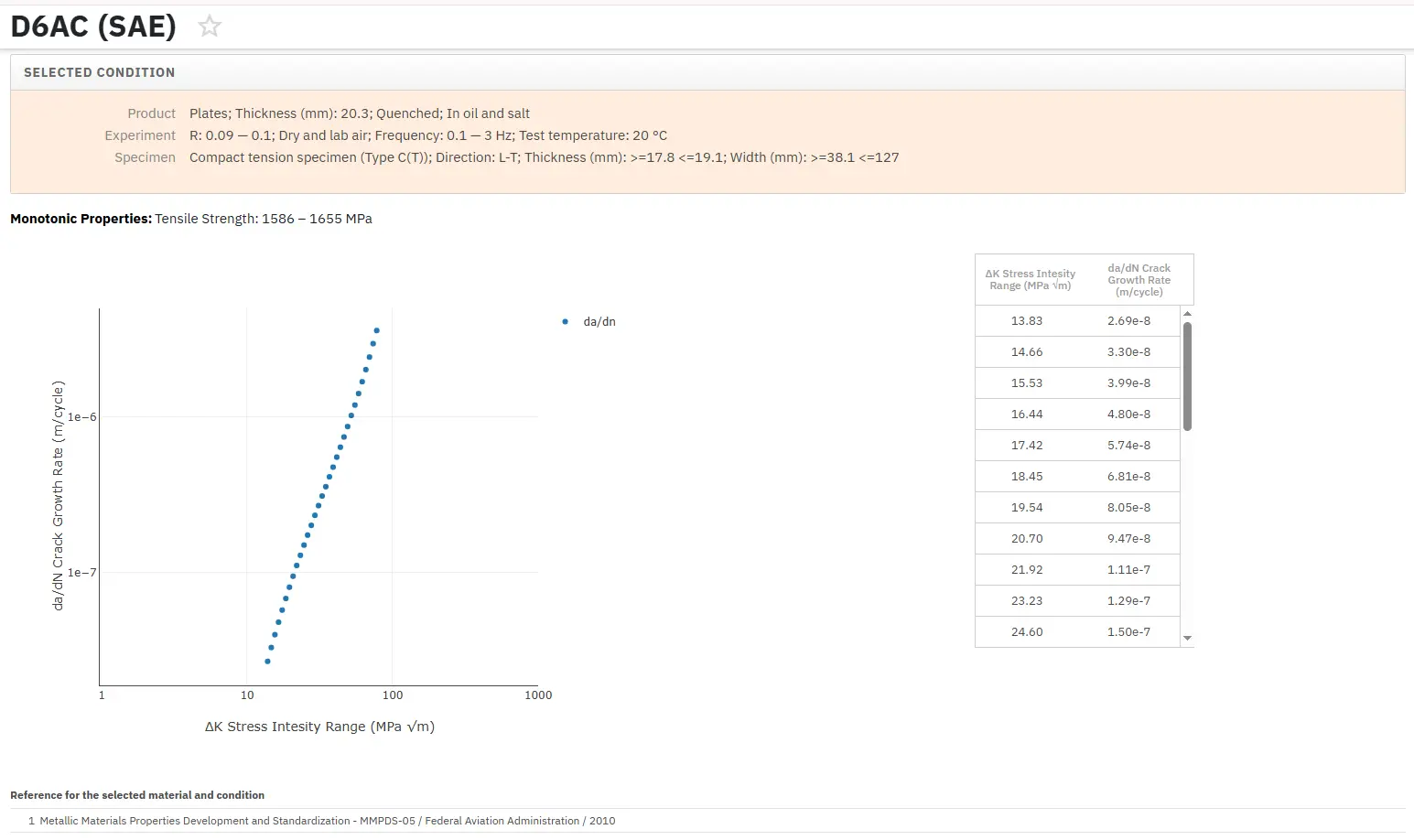
Access Fracture Mechanics Properties of Thousands of Materials Now!
Total Materia Horizon includes a unique collection of fracture mechanics properties such as K1C, KC, crack growth and Paris law parameters, for thousands of metal alloys and heat treatments.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.