Creep Life Prediction
Abstract
Creep life prediction is of paramount importance in selecting the right material for certain engineering applications and in the most extreme cases can prevent component failure leading to catastrophic effects.
Such implications mean that there has been an important development to assist in predicting creep life for example, the Strain-Acceleration-Parameter (SAP), which connects creep curves directly to the minimum creep rate.
An increasingly large number of engineering applications requires the choice of materials and design of components to be based, wholly or partially, on creep damage. The creep of materials is a significant engineering topic in many modern industries including power generation plants, chemical plants and the aerospace industry. The practical parameter of major importance is the prediction of the creep life of components subjected to elevated temperatures. Failure of these components may have catastrophic effects. Therefore, the development of methods for predicting the life of components operating within the creep regime has been an active research endeavor.
In the work of H. Sato and T. Miyno a method of creep life prediction by means of Strain-Acceleration-Parameter (SAP), α, is presented. The advantage of the proposed method is that the required parameters evaluated from individual creep curves are directly connected with the minimum creep rate.
It is widely accepted that creep behaviors are mainly evaluated by minimum or steady state creep rate. The important parameters are its stress dependence, grain size dependence and temperature dependence, and are characterized by the stress exponent, n, the grain size exponent, p, and the activation energy of creep, Qc. One of the general forms of equations that describe steady-state or minimum strain rates is the equation proposed by Mukherjee, et al.:
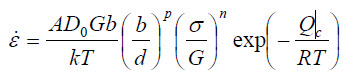 ... (1)
... (1)Here, A, D0, G, b, k and R are a constant, pre-exponential term of diffusion coefficient, shear modulus, the magnitude of Burgers vector, the Boltzmann's constant and the gas constant, respectively. The values T and σ are the absolute temperature and the applied stress which determine the creep conditions, and d is the grain size. The minimum creep rates are treated as the most important parameter describing creep behavior. The minimum creep rates, however, are evaluated from just a part of the creep curve, and the same minimum creep rates would be observed from creep curves whose shapes are different to each other.
For more precise determination and description of creep behavior, not only the minimum creep rates, but also the shape of creep curves should be considered.
The authors propose a characteristic value, Strain-Acceleration-Parameter (SAP), α, that reflects shape of creep curves and reflects acceleration of strain rate in secondary creep [6-7]:
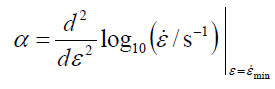 ... (2)
... (2)α corresponds to the curvature of the common logarithm of strain rate as a function of strain. The value is defined at a strain of minimum creep rate, εmin, and at a time of minimum creep rate, tmin.
Because it is the second order differential of strain, the values evaluated by means of simple finite differential vary and spread depending on the precision of calculation. To avoid this difficulty, authors applied least square spline interpolation for calculation of strain rate and related derivatives.
As the Strain-Acceleration-Parameter, α, is defined as a curvature of the common logarithm of strain rate as a function of strain, the creep curve can be extrapolated and reconstructed with suitable initial conditions. As α, is defined at minimum creep rate, and conditions at minimum creep rate, i.e., strain and strain-rate are known, the common logarithm of strain rate, logἑ, as a function of strain, ε, can be described as equation (3).
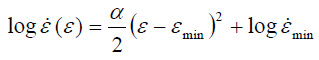 ... (3)
... (3)Here, min εmin and min ἑmin are evaluated experimentally from individual creep curves. Equation (3) can be solved numerically giving the creep curve, ε(t). Required values to reconstruct the whole creep curve are the SAP α, the minimum strain rate min ἑmin, the strain at minimum creep rate min εmin, and the time at minimum creep rate tmin. Three of these required four parameters directly correlate with a condition at the minimum creep rate.
Access Creep Properties of Thousands of Materials Now!
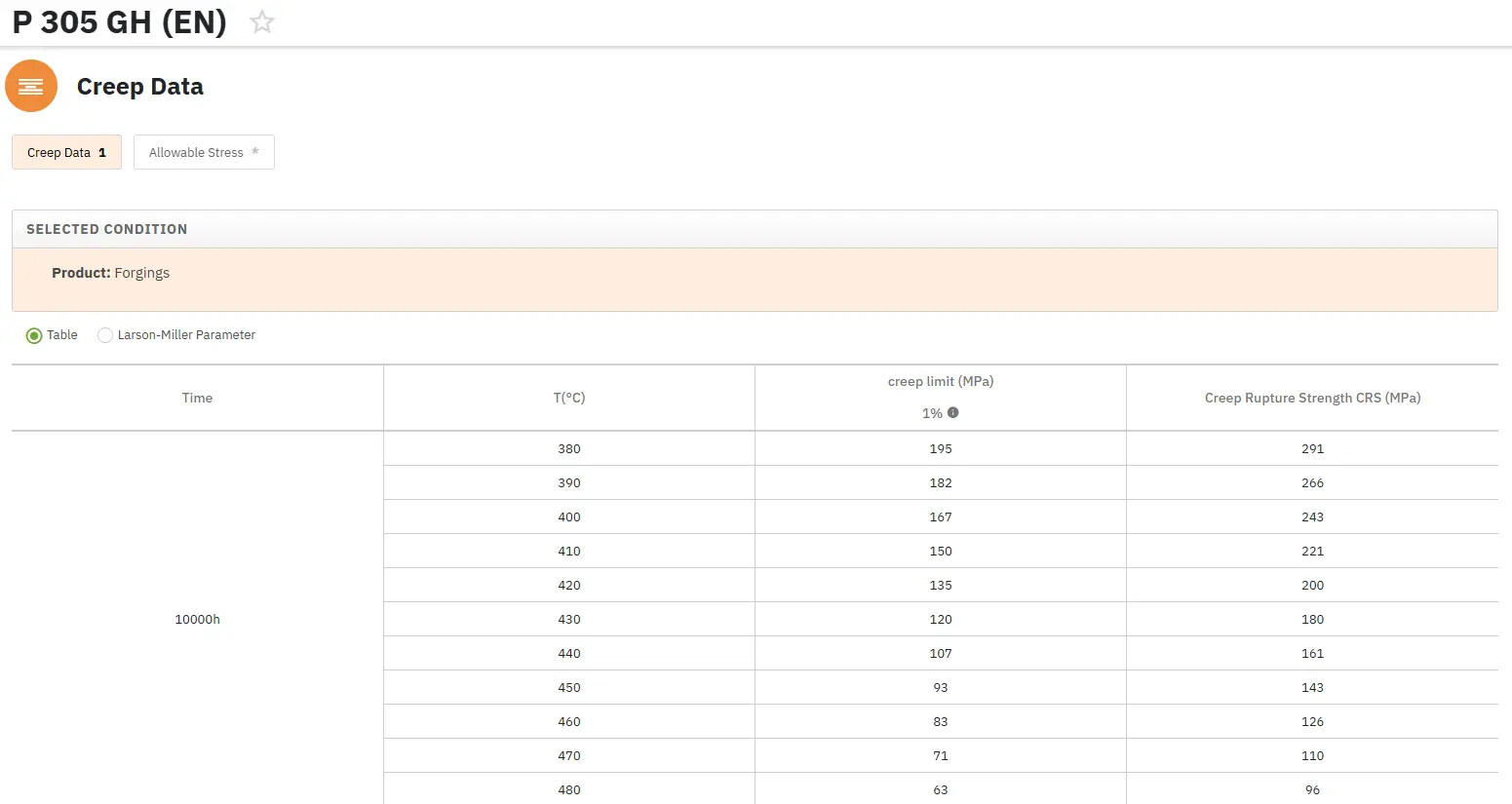
Total Materia Horizon includes the largest database of creep data such as yield stress and creep rupture strength at different temperatures, for thousands of metallic alloys and polymers.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.