Hardness Testing

The hardness of a material is a poorly defined term which has many meanings depending upon the experience of the person involved. In general, hardness usually implies a resistance to deformation, and for metals the property is a measure of their resistance to permanent or plastic deformation. To a person concerned with the mechanics of materials testing, hardness is most likely to mean the resistance to indentation, and to the design engineer it often means an easily measured and specified quantity which indicates something about the strength and heat treatment of the metal.

There are three general types of hardness measurements depending on the manner in which the test is conducted. These are:

Only indentation hardness is of major engineering interest for metals.

Scratch hardness is of primary interest to mineralogists. With this measure of hardness, various minerals and other materials are rated on their ability to scratch one another. Scratch hardness is measured according to the Mohs’ scale. This consists of 10 standard minerals arranged in the order of their ability lo be scratched. The softest mineral in this scale is talc (scratch hardness 1), while diamond has a hardness of 10. The Mohs’ scale is not well suited for metals since the intervals are not widely spaced in the high-hardness range. Most hard metals fall in the Mohs’ hardness range of 4 to 8.

In dynamic-hardness measurements the indenter is usually dropped onto the metal surface, and the hardness is expressed as the energy of impact. The Shore seleroscope, which is the commonest example of a dynamic-hardness tester, measures the hardness in terms of the height of rebound of the indenter.

Brinell Hardness

The first widely accepted and standardized indentation-hardness test was proposed by J. A. Brinell in 1900. The Brinell hardness test consists in indenting the metal surface with a 10-mm-diameter steel ball at a load of 3,000 kg mass (∼29400 N). For soft metals the load is reduced to 500 kg to avoid too deep an impression, and for very hard metals a tungsten carbide ball is used to minimize distortion of the indenter. The load is applied for a standard time, usually 30 s, and the diameter of the indentation is measured with a low-power microscope after removal of the load. The average of two readings of the diameter of the impression at right angles should be made.

The Brinell hardness number (BHN) is expressed as the load P divided by the surface area of the indentation. This is expressed by the formula:

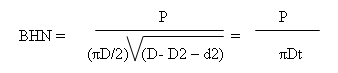
where
         P - applied load, N
         D - diameter of ball mm
         d - diameter of indentation, mm
         t - depth of the impression, mm

It will be noticed that the units of the BHN are MPa.

Unless precautions are taken to maintain P/D2 constant, which may be experimentally inconvenient, the BHN generally will vary with load. Over a range of loads the BHN reaches a maximum at some intermediate load. Therefore, it is not possible to cover with a single load the entire range of hardnesses encountered in commercial metals.

The relatively large size of the Brinell impression may be an advantage in averaging out local heterogeneities. Moreover, the Brinell test is less influenced by surface scratches and roughness than other hardness tests. On the other hand, the large size of the Brinell impression may preclude the use of this test with small objects or in critically stressed parts where the indentation could be a potential site of failure.

Meyer Hardness

Meyer suggested that a more rational definition of hardness than that proposed by Brinell would be one based on the projected area of the impression rather than the surface area. The mean pressure between the surface of the indenter and the indentation is equal to the load divided by the projected area of the indentation. Meyer proposed that this mean pressure should be taken as the measure of hardness. It is referred to as the Meyer hardness.

Like the Brinell hardness, Meyer hardness has units of MPa. The Meyer hardness is less sensitive to the applied load than the Brinell hardness. For a cold-worked material the Meyer hardness is essentially constant and independent of load, while the Brinell hardness decreases as the load increases. For an annealed metal the Meyer hardness increases continuously with the load because of strain hardening produced by the indentation. The Brinell hardness, however, first increases with load and then decreases for still higher loads. The Meyer hardness is a more fundamental measure of indentation hardness; yet it is rarely used for practical hardness measurements.

Meyer proposed an empirical relation between the load and the size of the indentation. This relationship is usually called Meyer’s law.

    P = kd^n’

The parameter n’ is the slope of the straight line obtained when log P is plotted against log d, and k is the value of P at d = 1. Fully annealed metals have a value of n’ of about 2.5, while n’ is approximately 2 for fully strain-hardened metals. This parameter is roughly related to the strain-hardening coefficient in the exponential equation for the true-stress-true-strain curve. The exponent in Meyer’s law is approximately equal to the strain-hardening coefficient plus 2.

Vickers Hardness

The Vickers hardness test uses a square-base diamond pyramid as the indenter. The included angle between opposite faces of the pyramid is 136°. This angle was chosen because it approximates the most desirable ratio of indentation diameter to ball diameter in the Brinell hardness test.

Because of the shape of the indenter, this is frequently called the diamond-pyramid hardness test. The diamond-pyramid hardness number (DPH), or Vickers hardness number (VHN, or VPH), is defined as the load divided by the surface area of the indentation. In practice, this area is calculated from microscopic measurements of the lengths of the diagonals of the impression. The DPH may be determined from the following equation:

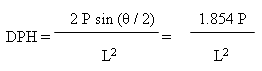
where
         P - applied load, kg
         L - average length of diagonals, mm
         θ - angle between opposite faces of diamond = 136°

The Vickers hardness test has received fairly wide acceptance for research work because it provides a continuous scale of hardness, for a given load, from very soft metals with a DPH of 5 to extremely hard materials with a DPH of 1,500. The Vickers hardness test is described in ASTM Standard E92-72.

Rockwell Hardness Test

The most widely used hardness test is the Rockwell hardness test. Its general acceptance is due to its speed, freedom from personal error, ability to distinguish small hardness differences in hardened steel, and the small size of the indentation, so that finished heat-treated parts can be tested without damage.

This test utilizes the depth of indentation, under constant load, as a measure of hardness. A minor load of 10 kg is first applied to seat the specimen. This minimizes the amount of surface preparation needed and reduces the tendency for ridging or sinking in by the indenter. The major load is then applied, and the depth of indentation is automatically recorded on a dial gage in terms of arbitrary hardness numbers.

The dial contains 100 divisions, each division representing a penetration of 0.00008 in (0.002 mm). The dial is reversed so that a high hardness, which corresponds to a small penetration, results in a high hardness number. This is in agreement with the other hardness numbers described previously, but unlike the Brinell and Vickers hardness designations, which have units of MPa, the Rockwell hardness numbers are purely arbitrary.

Major loads of 60, 100, and 150 kg are used. Since the Rockwell hardness is dependent on the load and indenter, it is necessary to specify the combination which is used. This is done by prefixing the hardness, number with a letter indicating the particular combination of load and indenter for the hardness scale employed. A Rockwell hardness number without the letter prefix is meaningless.

Hardened steel is tested on the C scale with the diamond indenter and a 150-kg major load. The useful range for this scale is from about RC 20 to RC 70. Softer materials are usually tested on the B scale with a 1/16-in-diameter steel ball and a 100-kg major load. The range of this scale is from RB 0 to RB 100. The A scale (diamond penetrator, 60-kg major load) provides the most extended Rockwell hardness scale, which is usable for materials from annealed brass to cemented carbides. Many other scales are available for special purposes.

The Rockwell hardness test is a very useful and reproducible one provided that a number of simple precautions are observed. Most of the points filled below apply equally well to the other hardness tests:

Microhardness Tests

Many metallurgical problems require the determination of hardness over very small areas. The measurement of the hardness gradient at a carburized surface, the determination of the hardness of individual constituents of a microstructure, or the checking of the hardness of a delicate watch gear might be typical problems. The use of a scratch-hardness test for these purposes was mentioned earlier, but an indentation-hardness test has been found to be more useful. The development of the Knoop indenter by the National Bureau of Standards and the introduction of the Tukon tester for the controlled application of loads down to 25 g have made micro hardness testing a routine laboratory procedure.

The Knoop indenter is a diamond ground to a pyramidal form that produces a diamond-shaped indentation with the long and short diagonals in the approximate ratio of 7:1 resulting in a state of plane strain in the deformed region. The Knoop hardness number (KHN) is the applied load divided by the unrecovered projected area of the indentation.

The special shape of the Knoop indenter makes it possible to place indentations much closer together than with a square Vickers indentation, e.g., to measure a steep hardness gradient. The other advantage is that for a given long diagonal length the depth and area of the Knoop indentation are only about 15 percent of what they would be for a Vickers indentation with the same diagonal length. This is particularly useful when measuring the hardness of a thin layer (such as an electroplated layer), or when testing brittle materials where the tendency for fracture is proportional to the volume of stressed material.

Hardness at Elevated Temperatures

Interest in measuring the hardness of metals at elevated temperatures has been accelerated by the great effort which has gone into developing alloys with improved high-temperature strength. Hot hardness gives a good indication of the potential usefulness of an alloy for high-temperature strength applications.

In an extensive review of hardness data at different temperatures, Westbrook showed that the temperature dependence of hardness could be expressed by

    H = Ae^-BT

where
         H = hardness, kg/mm²
         T = test temperature, K
         A,B constants

Plots of log H versus temperature for pure metals generally yield two straight lines of different slope. The change in slope occurs at a temperature which is about one-half the melting point of the metal being tested. Similar behavior is found in plots of the logarithm of the tensile strength against temperature. Above mentioned figure shows this behavior for copper. It is likely that this change in slope is due to a change in the deformation mechanism at higher temperature.

The constant A derived from the low-temperature branch of the curve can be considered to be the intrinsic hardness of the metal, that is, H at 0 K. Westbrook correlated values of A for different metals with the heat content of the liquid metal at the melting point and with the melting point. This correlation was sensitive to crystal structure.

The constant B, derived from the slope of the curve, is the temperature coefficient of hardness. This constant was related in a rather complex way to the rate of change of heat content with increasing temperature. With these correlations it is possible to calculate fairly well the hardness of a pure metal as a function of temperature up to about one-half its melting point.