Design for High-Temperature Applications: Part One
Abstract
Time-dependent deformation and fracture of structural materials at elevated temperatures are among the most challenging engineering problems faced by materials engineers.
In order to develop an improved design methodology for machines and equipment operating at high temperatures, several key concepts and their synergism must be understood: plastic instability at elevated temperatures, deformation mechanisms and strain components associated with creep processes, stress and temperature dependence, fracture at elevated temperatures, environmental effects.
Apart from nineteenth-century steam boilers, machines and equipment for high-temperature operation have been developed principally in the 20th century. Energy conversion systems based on steam turbines, gas turbines, high-performance automobile engines, and jet engines provide the technological foundation for modern society.
All of these machines have in common the use of metallic materials at temperatures where time-dependent deformation and fracture processes must be considered in their design. The single valued time-invariant strain associated with elastic or plastic design analysis in low-temperature applications is not applicable, nor is there in most situations a unique value of fracture toughness that may be used as a limiting condition for part failure. In addition to the phenomenological complexities of time-dependent behavior, there is now convincing evidence that the synergism associated with gaseous environmental interactions may have a major effect, in particular on high-temperature fracture.
Basic Concepts of Elevated-Temperature Design. Time-dependent deformation and fracture of structural materials at elevated temperatures are among the most challenging engineering problems faced by materials engineers. In order to develop an improved design methodology for machines and equipment operating at high temperatures, several key concepts and their synergism must be understood:
- Plastic instability at elevated temperatures
- Deformation mechanisms and strain components associated with creep processes
- Stress and temperature dependence
- Fracture at elevated temperatures
- Environmental effects.
The issues of interest from a design basis are the nature of primary creep, the validity of the concept of viscous steady-state creep, and the dependence of deformation on both temperature and stress. The simplest and most pervasive idea in creep of metals is an approach to an equilibrium microstructural and mechanical state. Thus a hardening associated with dislocation generation and interaction is countered by a dynamic microstructural recovery or softening. This process proceeds during primary creep and culminates in a steady-state situation.
Plastic Instability
A major issue in the tensile creep test is the role of plastic instability in leading to tertiary creep. Understanding of the nature of plastic instability for time-dependent flow has depended on the theory of Hart. He showed that the condition for stable deformation is:
γ + m ≥ 1
where:
m is the strain-rate sensitivity, and
γ, is a measure of the strain-hardening rate.
For steady-stale flow, γ is equal to 0. For constant stress tests, Burke and Nix concluded that flow must be unstable when steady state is reached according to Hart’s criterion but that macroscopic necking is insignificant and that the flow remains essentially homogeneous. They concluded that a true steady state does exist. Hart himself questioned the conclusions based on their analysis but did not rule out the possibility of a steady state for pure metals.
In a very careful experimental analysis, Wray and Richmond later concluded that the concept of a family of steady states is valid. Tests were performed in which two of the basic parameters (stress, strain rate, and temperature) are held constant. However, they reported the intrusion of nonuniform deformation before the steady state was reached. They also pointed out the complexities associated with uncontrolled and often unmeasured loading paths, which produce different structures at the beginning of the constant stress or constant strain rate portions of the test. For constant stress tests in pure metals, although the concept of steady state is appealing, it appears not yet to have been rigorously demonstrated.
In constant load tests, steady-state behavior would of course result in an increasing creep rate after the minimum, as the true stress increases. As such, the test is inappropriate to evaluate the concept. However, it is by far the most common type of creep test and can be analyzed for instability.
Creep Processes
Creep behavior can be characterized either in terms of deformation mechanisms or in terms of strain constituents.
Deformation Mechanisms. Creep of metals is primarily a result of the motion of dislocations, but is distinct from time-independent behavior in that flow continues as obstacles, which may be dislocation tangles or precipitate particles, are progressively overcome. The rate-controlling step involves diffusion to allow climb of edge dislocations or cross slip of screw dislocations around obstacles. In steady-state theory, there is a balance between the hardening associated with this dislocation motion and interaction, and a dynamic recovery associated with the development of a dislocation substructure.
Theory for such a process predicts a power-law dependence of creep rate on applied stress. At very high homologous temperatures (T/Tm) and low stresses, creep may occur in both metals and ceramics by mass transport involving stress-directed flow of atoms from regions under compression to regions under tension. In this case, theory i ndicates that there is a stress dependence of unity and that the process is controlled either by bulk diffusion or by grain-boundary diffusion. These various processes of creep (dislocation controlled as well as diffusion controlled) may be represented on a deformation mechanism map to highlight regimes of stress and temperature where each mechanism, based on current theories, may be operating. However, such maps are only as good as the theories on which they are based and give no guidance on deformation path dependence.
Another important deformation process in metallic and ionic polycrystals at high temperature and low stresses is grain-boundary sliding. The resistance to sliding is determined by the mobility of grain-boundary dislocations and by the presence of hard particles at the boundary. This sliding leads to stress concentrations at grain junctions, which are important in nucleating cracks. In ductile materials, these stress concentrations may be relieved by creep and stress relaxation in the matrix or by grain-boundary migration.
Strain Components. There are several different sources of strain at high temperature in response to an applied stress. The elastic strain is directly proportional to stress, and a modulus that is temperature dependent can be determined. For metallic materials and ceramics, although there is a strain-rate dependence of elastic modulus, it is small and often ignored. Plastic strain for all materials may be treated as three separate constituents:
- Time-independent nonrecoverable, which may be thought of as an instantaneous deformation
- Time-dependent nonrecoverable, which may involve any or all of the micromechanisms described above
- Time-dependent recoverable.
The first of these is unlikely to be significant in practical applications except in the region of stress concentrations since loading is normally well below the macroscopic yield stress. The second is the major source of creep in normal laboratory testing. The third constituent is not widely studied or analyzed, but may become very important at low stresses and under nonsteady conditions, that is, high-temperature service. It leads to what has been termed creep recovery and anelasticity.
At high temperatures, the application of a stress leads to creep deformation resulting from the motion of dislocations, mass transport by diffusion, or grain-boundary sliding. These processes in turn lead to a distribution of internal stresses that may relax on removal of the stress. In metals it is associated with the unbowing of pinned dislocations, rearrangement of dislocation networks, and local grain-boundary motion.
Whereas the importance of creep recovery is well recognized in polymer design, it has often been ignored in design of metallic and ceramic materials. A few extensive studies have been reported on metals that have led to several broad conclusions:
- Creep-recovery strain increases linearly with stress for a fixed time at a given temperature, but is dependent on prestrain.
- The rate of creep recovery increases with increasing temperature.
- When the stress is low enough, essentially all transient creep is linear with stress and recoverable.
- Mathematically, the recovery may be described by a spectrum of spring dashpot combinations with a wide range of relaxation times.
Stress and Temperature Dependence
The minimum creep rate in both constant load and constant stress tests is normally represented by a power function of stress, and the temperature by an Arrhenius e xpression including an activation energy term (Q) derived from chemical reaction rate theory:
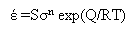
where S, which is a constant, depends on structure. Although an exponential or hyperbolic sine stress function may provide a better fit in some cases, the power function has generally prevailed and has become strongly linked with mechanistic treatments.
Access Creep Properties of Thousands of Materials Now!
Total Materia Horizon includes the largest database of creep data such as yield stress and creep rupture strength at different temperatures, for thousands of metallic alloys and polymers.
Get a FREE test account at Total Materia Horizon and join a community of over 500,000 users from more than 120 countries.