True Stress - True Strain Curve: Part Two

The engineering stress-strain curve does not give a true indication of the deformation characteristics of a metal because it is based entirely on the original dimensions of the specimen, and these dimensions change continuously during the test. Also, ductile metal which is pulled in tension becomes unstable and necks down during the course of the test.

Because the cross-sectional area of the specimen is decreasing rapidly at this stage in the test, the load required continuing deformation falls off. The average stress based on original area likewise decreases, and this produces the fall-off in the stress-strain curve beyond the point of maximum load. Figure 1 shows the true stress-strain curves in tension at room temperature for various metals.

Figure 1: True stress-strain curves in tension at room temperature for various metals

Actually, the metal continues to strain-harden all the way up to fracture, so that the stress required to produce further deformation should also increase. If the true stress, based on the actual cross-sectional area of the specimen, is used, it is found that the stress-strain curve increases continuously up to fracture. If the strain measurement is also based on instantaneous measurements, the curve, which is obtained, is known as a true-stress-true-strain curve. This is also known as a flow curve since it represents the basic plastic-flow characteristics of the material.

Any point on the flow curve can be considered the yield stress for a metal strained in tension by the amount shown on the curve. Thus, if the load is removed at this point and then reapplied, the material will behave elastically throughout the entire range of reloading.

The true stress s is expressed in terms of engineering stress s by

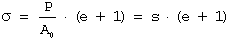(1)

The derivation of Eq. (1) assumes both constancy of volume and a homogenous distribution of strain along the gage length of the tension specimen. Thus, Eq. (1) should only be used until the onset of necking. Beyond maximum load the true stress should be determined from actual measurements of load and cross-sectional area.

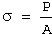(2)

The true strain e may be determined from the engineering or conventional strain e by

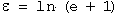(3)

Figure 2. Comparison of engineering and true stress-strain curves

This equation is applicable only to the onset of necking for the reasons discussed above. Beyond maximum load the true strain should be based on actual area or diameter measurements.

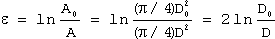(4)

Figure 1 compares the true-stress-true-strain curve with its corresponding engineering stress-strain curve. Note that because of the relatively large plastic strains, the elastic region has been compressed into the y-axis. In agreement with Eqs. (1) and (3), the true-stress-true-strain curve is always to the left of the engineering curve until the maximum load is reached. However, beyond maximum load the high-localized strains in the necked region that are used in Eq. (4) far exceed the engineering strain calculated from Eq. (1).

Frequently the flow curve is linear from maximum load to fracture, while in other cases its slope continuously decreases up to fracture. The formation of a necked region or mild notch introduces triaxial stresses, which make it difficult to determine accurately the longitudinal tensile stress on out to fracture.