Property Control in Production of Aluminum Sheet: Part Three
Abstract
At sufficiently high coiling temperature and time after hot rolling a fully recrystallized grain structure is usually generated by self-annealing, i.e. a fully soft (O-temper) condition is achieved. During subsequent cold rolling strain hardening significantly increases flow stress and reduces formability. Furthermore, the change from cube to a rolling texture implies a diametrical anisotropy behavior, which can be noted in deep drawn cups.
by Jürgen Hirsch et al.
At sufficiently high coiling temperature and time after hot rolling a fully recrystallized grain structure is usually generated by self-annealing, i.e. a fully soft (O-temper) condition is achieved. During subsequent cold rolling strain hardening significantly increases flow stress and reduces formability, as can be seen in Figure 1a. Furthermore, the change from cube to a rolling texture implies a diametrical anisotropy behavior, which can be noted in deep drawn cups (Figure 1b, c).
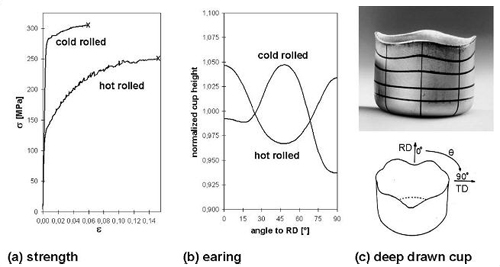
Figure 1: (a) Flow stress and (b), (c) anisotropy (earing) in hot and cold rolled Al-sheet.
Yield strength evolution of different materials is shown in Figure 2a as measured by tensile tests performed on cold rolled material for a number of different rolling strains and alloys. The tensile data can be represented by the generalized Voce equation. Also, a dependence of the Voce parameters on alloy composition can be formulated, which allows interpolating such data for different alloys.
After strain hardening and subsequent annealing the material undergoes recovery due to annihilation of dislocations and dislocation re-arrangement; thus, strength is lowered. Figure 2b shows the effect of recovery on yield strength during annealing.
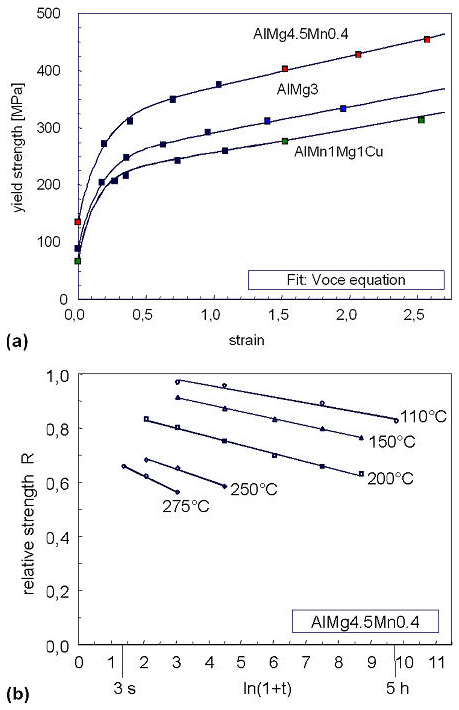
Figure 2: Modeling of (a) strain hardening for various Al-Mg alloys and (b) recovery in AlMg5Mn for different annealing temperatures.
An important practical application is the correct prediction of strength evolution of Al alloys under plant rolling conditions. Here always elevated temperatures (>100°C) occur during and after cold rolling due to the high reduction and speed of industrial rolling mills. So, in multi-pass cold rolling sequences the coil requires cooling periods to avoid too high temperature levels in subsequent passes. As a consequence, the coil is stored for several hours before the subsequent rolling pass while the temperature generated by the previous pass gradually decreases and recovery takes place to some extent, depending on alloy, constitution, exit temperature, cooling conditions and previous pass reductions.
For example on a two-stand tandem mill the succession of two rapid passes with short intermediate time, followed by a long coil storage period before the material is brought to the next passes, bestows complex conditions where the strength of the alloy and the processing conditions strongly interact. Figure 3 shows the strength prediction of three double-passes on such a mill. It is demonstrated that at 50% reduced rolling speed the final yield strength is increased by 20 MPa as a result of increased cooling periods in-between stands and lower coil storage temperatures.
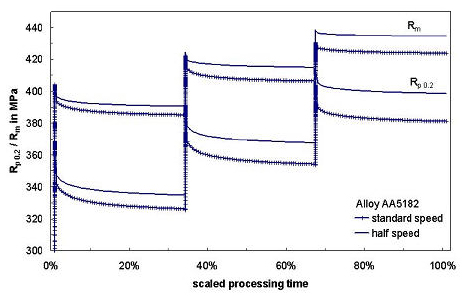
Figure 3: Simulated cold rolling schedule on a two-stand tandem mill (three double passes) for two different processing speeds.
Formability of Aluminum Sheets
The conventional way to simulate sheet forming operations like deep drawing is to employ the finite element method (FEM). In order to account for crystallographic texture, the material input to the FEM code – the so-called constitutive equations – must incorporate the anisotropic properties of the sheet.
For this purpose, two methods are mainly used. In the first method, the plastic behavior is described by a phenomenological yield function. However, although such yield criteria can readily be implemented into FEM codes, the accuracy achieved with this method is generally not satisfactory. In the second approach, a polycrystal texture is associated with each element of the FE-mesh and texture, hardening and anisotropy are updated as deformation proceeds. Thus, the constitutive behavior is derived from polycrystal plasticity. However, these FEM computations are extremely time consuming, which currently restrains their use from routine forming simulations.
In order to take advantage of both approaches it has been proposed to use an anisotropic yield locus, derived from the sheet texture, as an input to the FEM code. Figure 4 shows the yield locus of AA 6181 car body sheet in the final solutionized T4 temper.
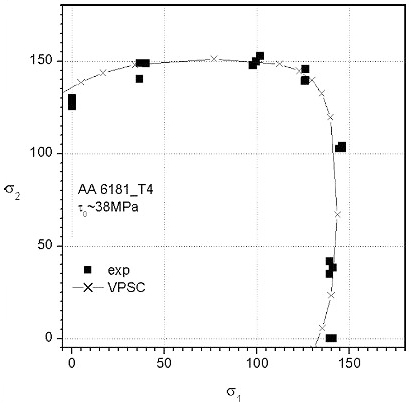
Figure 4: Yield surface of solution annealed AA 6181 car body sheet, plotted in the σ1/σ2 plane.
The yield surface was derived from the texture data with the VPSC formulation by probing the texture with equi-spaced strain rates contained in a given plane through the full five-dimensional stress space. Here, the conventional plane spanned by the two in-plane stresses σ1 and σ2 is used assuming that the through-thickness stress σ3 is zero. Finally, the data are normalized with the critical resolved shear stress, τ0. The texture derived yield surface fits very well with the experimental data points for uniaxial tensile tests in rolling and transverse direction as well as for different combinations of biaxial stretching.
Мгновенный доступ к тысячам металлографических изображений!
Total Materia Horizon содержит уникальную коллекцию металлографических изображений различных сплавов, стандартов и термических обработок.
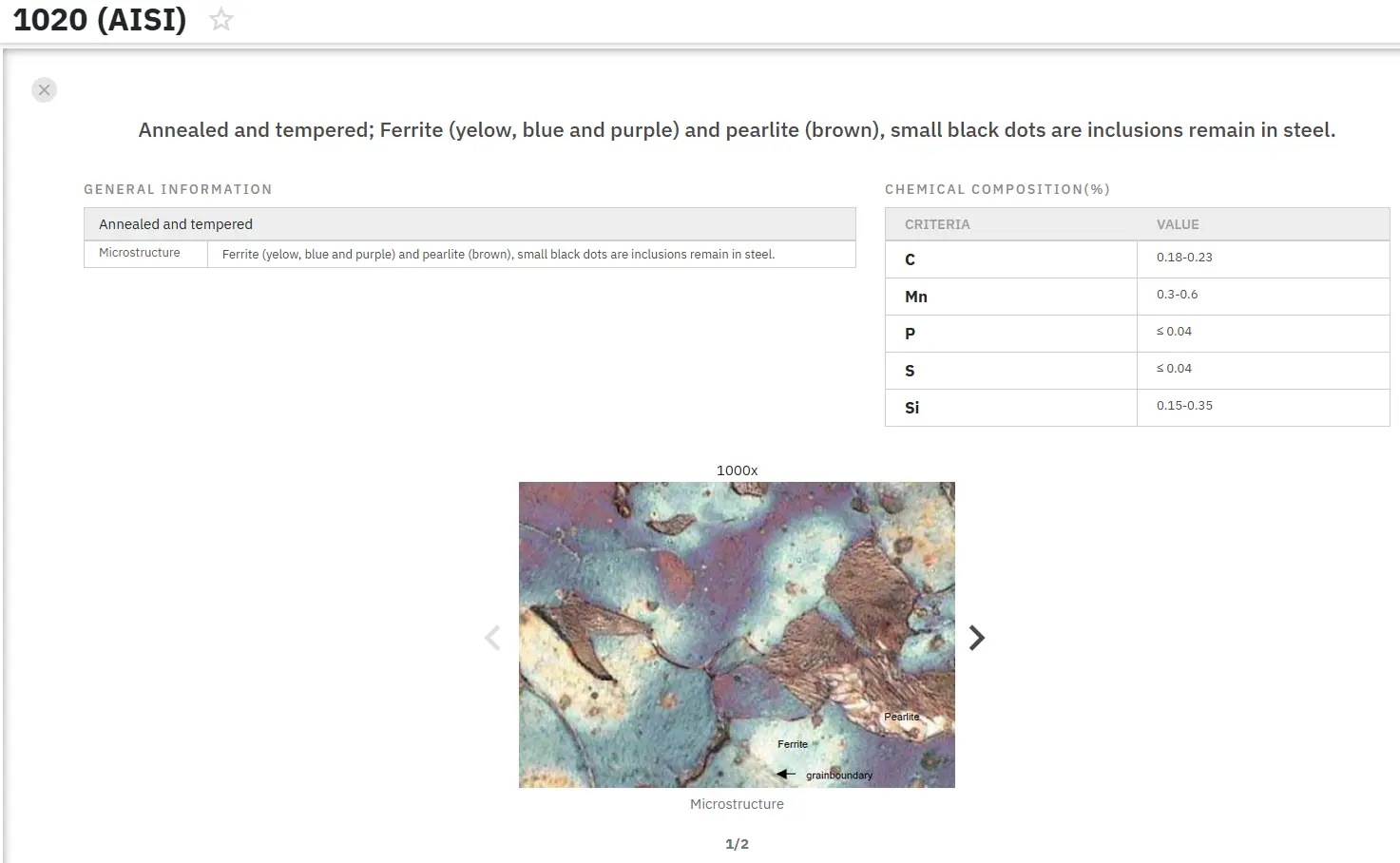
Получите бесплатный тестовый аккаунт в Total Materia Horizon и присоединяйтесь к сообществу из более чем 500 000 пользователей из 120+ стран.