Spinodal Decomposition of Non-ferrous Alloys: Part One
Abstract
Spinodal decomposition manifests itself as characteristic patterns in an alloy, which are a direct result of phase separation during the quenching process.
As an example of homogenous isostructural transformation, spinodal decomposition is diffusion driven and occurs for unstable states.
Alloys are composite materials which are formed by mixing a number of pure metals together at a high temperature and then rapidly quenching or cooling the mixture to form a solid. During the process of quenching, the components undergo a phase seperation in which they begin to form patterns. These pattern formations can be divided into two classes: Nucleation and Spinodal Decomposition. Qualitatively nucleation occurs when the individual components begin to materialize from the homogenous mixture as isolated droplets or bubbles.
Spinodal decomposition is an example of a homogenous isostructural transformation that is diffusion driven and occurs for unstable states. The global composition during the transformation is constant, but increasing composition fluctuations lead to formation of domains separated by diffuse interfaces. For diffusion-driven processes, also called thermally-driven processes, a certain temperature is needed for the transformation.
A sufficient temperature will make the formation of a vacancy and a jump (in the case of vacancy diffusion) of an atom possible. Spinodal decomposition occurs for states with a negative second derivative of the free energy with respect to composition, i.e. states within the chemical spinodal region in a miscibility gap in a phase diagram. Within the miscibility gap, a coherent miscibility gap and a coherent spinodal is defined if the equilibrium domains possess different elastically properties or lattice parameters. The coherent spinodal is narrower both in temperature and compositional extension compared to the chemical spinodal.
The coherent spinodal takes into account the decrease in free energy due to formation of coherent strain. In Figure 1(a), the effect of different compositional wavelengths and amplitudes on the change in free energy is shown for a binary mixture of equal amounts of A and B atoms inside a symmetric spinodal regime. A symmetric spinodal regime has its peak value of the free energy at A0.5B0.5. As shown, any wavelengths larger than the critical wavelength (indicated by an arrow in the figure) that grows in amplitude will decrease the free energy. No nucleus is needed, as shown by the dotted states at zero amplitude. For shorter wavelength than the critical wavelength, the free energy increases as the amplitude of the wave increases.
The free energy valley becomes deeper for longer wavelengths. In the initial state of spinodal decomposition high frequencies are reduced, and any wavelength larger than the critical will grow, i.e. the compositional fluctuation purifies. But, as seen from the figure every wavelength is associated with a specific free energy value; in order to decrease the total free energy a longer wavelength need to develop and grow on the expense of shorter ones, that will decay in amplitude and vanish. Hence the free energy decrease of the longer wavelength will cover the cost for the shorter wavelength to decay. An infinite wavelength would give the largest free energy decrease, but would involve long range diffusion. The fastest growing wavelength is determined by the free energy decrease and the energy needed for the diffusion length considered.
In Figure 1 (b), the free energy change due to different wavelengths and amplitudes are shown for a binary system, with an off peak composition inside a symmetric spinodal region. In this case, there exist wavelengths smaller than the critical one where a free energy decrease can occur by nucleation. The nuclei increase their amplitude, to reach the free energy valley. As in the case of symmetric composition, for wavelengths larger than the critical, the system decreases its energy without any energy barrier as the amplitude increases. As one moves from the center of the spinodal region towards the spinodal line the critical wavelength increases and hence probability for nucleation increases. As mentioned already, at the spinodal line the wavelength is infinite, and outside the spinodal line phase transformation occurs by nucleation and growth.
The critical wavelength does not only vary with composition, but also with temperature. The critical wavelength decreases with temperature, resulting in a maximum driving force for decomposition at the bottom of the miscibility gap, for the composition at the peak of the free energy. On the other hand, the diffusion is faster at higher temperatures, and therefore the transformation rate goes through a maximum for a certain temperature, usually far up in the spinodal regime.
In summary, the critical wavelength varies within the spinodal regime. Systems with compositions at the peak of the free energy are unstable against any fluctuation larger than the critical wavelength, and off peak compositions possess a degree of metastability since for short wavelengths fluctuations an energy barrier is needed to overcome to reach the decreased free energy state, i.e. a nucleus needs to form. The metastability increases with temperature.
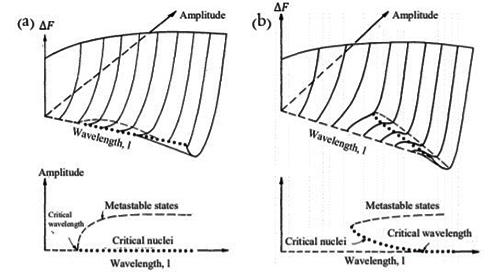
Figure 1: (a) Symmetric composition in a symmetric spinodal. (b) Asymmetric composition in a symmetric spinodal. Free energy of a system with spinodal decomposition in terms of amplitude and wavelength. The dots represent the critical nucleus depending on the wavelength. The dashed lines show the metastable states. The metastable states can be reached for wavelengths longer than the critical without any barrier in the free energy. (a) Any wavelength above the critical will grow. A longer wavelength grows and ends deeper in the free energy valley, but a certain wavelength is always connected with a specific end value of the free energy. To decrease the free energy longer wavelengths need to grow on the expanse of shorter. (b) For an asymmetric composition in a symmetric miscibility gap there exists wavelengths where a critical nucleus can be formed by overcoming an energy barrier. For wavelengths larger than a critical no energy barrier exists.
立即查看数万种材料的热处理曲线!
Total Materia Horizon 包含上数万种材料的热处理细节、淬透性曲线、硬度回火曲线、TTT 曲线和 CCT 曲线 等。
申请 Total Materia Horizon免费试用帐户,加入来自全球 120 多个国家超过 500,000 名用户的大家庭。