Creep Life Prediction Using Strain-Acceleration-Parameter (SAP) Method
Abstract
Creep life prediction plays a crucial role in material selection for high-temperature engineering applications and prevents catastrophic component failures. This research presents the Strain-Acceleration-Parameter (SAP) method, which directly connects creep curves to minimum creep rate for enhanced prediction accuracy. The SAP approach addresses limitations of traditional methods by considering both minimum creep rates and complete creep curve shapes. This methodology provides engineers with improved tools for predicting component life in critical applications such as power generation, chemical processing, and aerospace industries, where elevated temperature operations demand precise creep behavior assessment.
Introduction to Creep Life Prediction
Modern engineering applications increasingly require material selection and component design based entirely or partially on creep damage considerations. Creep behavior represents a significant engineering challenge across multiple industries, including power generation plants, chemical processing facilities, and aerospace manufacturing. The practical parameter of paramount importance remains the accurate prediction of creep life for components operating under elevated temperatures.
Component failure in these critical applications can result in catastrophic consequences, making the development of reliable life prediction methods an essential research priority. Traditional approaches often fall short in providing comprehensive creep behavior assessment, necessitating advanced methodologies that consider multiple creep parameters simultaneously.
Understanding Minimum Creep Rate and Its Limitations
The engineering community widely accepts that creep behaviors are primarily evaluated through minimum or steady-state creep rate analysis. The fundamental parameters characterizing creep behavior include stress dependence, grain size dependence, and temperature dependence, represented by the stress exponent (n), grain size exponent (p), and activation energy of creep (Qc), respectively.
Mukherjee and colleagues proposed one of the most recognized equations describing steady-state or minimum strain rates:
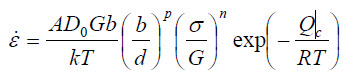
In this equation, A represents a material constant, D₀ is the pre-exponential term of the diffusion coefficient, G denotes shear modulus, b indicates the magnitude of Burgers vector, k represents Boltzmann's constant, and R signifies the gas constant. The variables T and σ represent absolute temperature and applied stress, respectively, which determine creep conditions, while d represents grain size.
While minimum creep rates serve as the most important parameter describing creep behavior, they represent only a portion of the complete creep curve. Identical minimum creep rates can be observed from creep curves with significantly different shapes, limiting the precision of traditional prediction methods.
The Strain-Acceleration-Parameter (SAP) Method
Enhanced Creep Curve Analysis
For more precise determination and comprehensive description of creep behavior, both minimum creep rates and complete creep curve shapes must be considered. The Strain-Acceleration-Parameter (SAP) method addresses this limitation by introducing a characteristic value, α, that reflects both creep curve shape and strain rate acceleration during secondary creep.
The SAP is defined mathematically as:
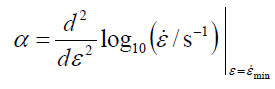
The parameter α corresponds to the curvature of the common logarithm of strain rate as a function of strain. This value is specifically defined at the strain of minimum creep rate (εₘᵢₙ) and at the time of minimum creep rate (tₘᵢₙ).
Computational Considerations
Since SAP represents the second-order differential of strain, values calculated using simple finite differential methods can vary significantly and spread depending on calculation precision. To overcome this computational challenge, researchers applied least square spline interpolation for calculating strain rate and related derivatives, ensuring more accurate and consistent results.
Creep Curve Reconstruction and Extrapolation
Mathematical Framework
The Strain-Acceleration-Parameter α enables creep curve extrapolation and reconstruction with appropriate initial conditions. Since α is defined at minimum creep rate, and conditions at minimum creep rate (strain and strain-rate) are known, the common logarithm of strain rate (log ε̇) as a function of strain (ε) can be described using the following relationship:
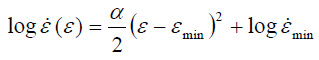
Here, εₘᵢₙ and ε̇ₘᵢₙ are determined experimentally from individual creep curves. Equation (3) can be solved numerically, yielding the complete creep curve ε(t).
Required Parameters for Curve Reconstruction
Complete creep curve reconstruction requires four essential parameters:
- The Strain-Acceleration-Parameter (α)
- The minimum strain rate (ε̇ₘᵢₙ)
- The strain at minimum creep rate (εₘᵢₙ)
- The time at minimum creep rate (tₘᵢₙ)
Significantly, three of these four required parameters directly correlate with conditions at the minimum creep rate, establishing a strong foundation for accurate prediction methodology.
Applications in Engineering Industries
Power Generation Industry
In power generation facilities, components such as turbine blades, steam pipes, and pressure vessels operate under extreme temperature conditions for extended periods. The SAP method provides enhanced prediction accuracy for these critical components, enabling better maintenance scheduling and replacement planning.
Chemical Processing Applications
Chemical plants require materials that can withstand corrosive environments at elevated temperatures. The comprehensive creep curve analysis offered by the SAP method supports more informed material selection and component design decisions.
Aerospace Engineering
Aircraft engines and spacecraft components face unique challenges combining high temperatures, stress concentrations, and weight limitations. The SAP methodology's ability to predict complete creep behavior makes it particularly valuable for these demanding applications.
Advantages of the SAP Method
The Strain-Acceleration-Parameter approach offers several distinct advantages over traditional creep life prediction methods:
Enhanced Accuracy: By considering complete creep curve shapes rather than just minimum creep rates, the SAP method provides more comprehensive behavior prediction.
Direct Parameter Connection: Required parameters are directly connected to minimum creep rate conditions, simplifying experimental determination and reducing uncertainty.
Improved Reliability: The method's consideration of strain rate acceleration during secondary creep enhances long-term prediction reliability.
Practical Implementation: The four-parameter approach balances computational complexity with practical usability for engineering applications.
Conclusion
The Strain-Acceleration-Parameter method represents a significant advancement in creep life prediction technology. By addressing the limitations of traditional approaches that rely solely on minimum creep rates, the SAP method provides engineers with a more comprehensive tool for predicting component behavior under elevated temperature conditions.
This methodology's ability to reconstruct complete creep curves from experimentally determined parameters makes it particularly valuable for critical engineering applications where component failure can have catastrophic consequences. As industries continue to push the boundaries of operating conditions, advanced prediction methods like SAP become increasingly essential for ensuring safe and reliable operation.
The continued development and refinement of creep life prediction methods will remain crucial for advancing engineering capabilities in power generation, chemical processing, aerospace, and other high-temperature applications.
立即获取数万种材料的蠕变性能!
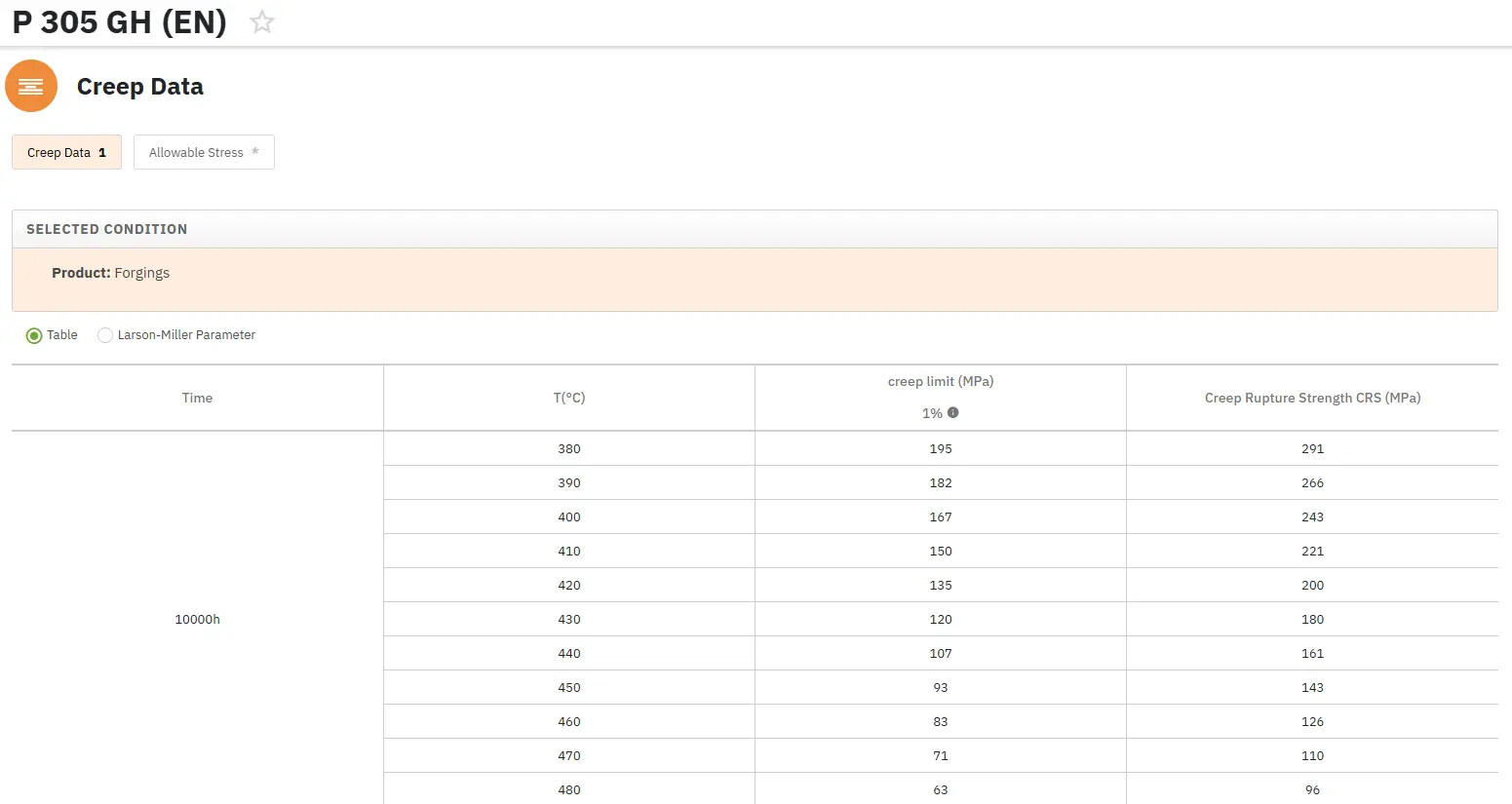
Total Materia Horizon 包含最大的蠕变数据集,包括数万种金属合金和聚合物在不同温度下的屈服应力和蠕变断裂强度。
申请 Total Materia Horizon免费试用帐户,加入来自全球 120 多个国家超过 500,000 名用户的大家庭。