Fracture

---

Understanding Ductile Fracture Mechanisms

A pure, inclusion-free metal can elongate under tension to achieve approximately 100% reduction in area (RA) and exhibit point fracture, as demonstrated in Fig. 1. However, most alloys contain second phases that lose cohesion with the matrix or fracture, creating voids that expand as dislocations flow into them. The coalescence of these voids forms a continuous fracture surface, followed by failure of the remaining material annulus, usually occurring on a plane positioned at 45° to the tension axis.

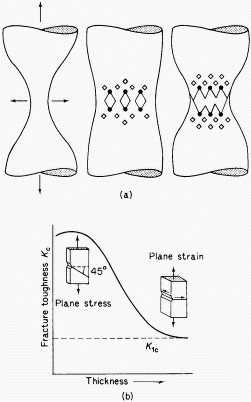
Figure 1: (a) Stages in ductile fracture from inclusions and (b) Fracture toughness n thickness

The central fracture surface consists of numerous cup-like depressions commonly referred to as dimples. The shape of these dimples is strongly influenced by the direction of major stresses, appearing circular under pure tension and parabolic under shear conditions. Dimple size depends largely on the number of inclusion sites present in the material.

Figure 2a) below illustrates typical dimple formations in ductile fracture.

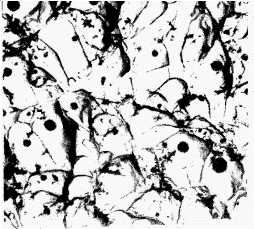
Figure 2a): Dimples in a ductile fracture of mild steel (x5000)

Several important characteristics define ductile fracture behavior. Pure metals and solid solutions that remain relatively free from second-phase particles, including impurity particles, typically demonstrate greater ductility compared to strong two-phase alloys. The local stress required for void nucleation at particles depends on their resistance to cracking and the strength of their bond with the matrix material.

The local stress generated at particles correlates with the flow strength of the alloy, the applied strain, and the shape and size of the particles themselves. Growth of holes that eventually coalesce to form macroscopic fracture depends on the applied stresses being tensile in nature. Significantly higher ductilities can be achieved through compressive straining processes.

Cleavage and Intercrystalline Fracture Patterns

In cleavage fracture, the material fails along well-defined crystallographic planes within individual grains, though the crack path experiences influence from grain boundaries and inclusions. A cleavage fracture surface contains large smooth areas separated by cleavage steps and feathers, river markings, and cleavage tongues, which result directly from crack path disturbances, as shown in Figure 2b) below.

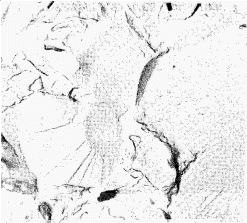
Figure 2b): Cleavage patterns in HS steel fracture (x12000)

Intercrystalline fracture is characterized by grain separation that reveals a surface composed of grain boundary facets, illustrated in Fig. 2c. This fracture type commonly occurs in stress-corrosion scenarios, creep conditions, hot tearing, and hydrogen embrittlement situations.

Figure 2c): Intergranular fracture in low alloy steel (x1500)

Fatigue fractures display characteristic striations (Fig. 2d) that represent the extent of crack propagation under each loading cycle. These patterns provide valuable insight into the cyclic loading history experienced by the material.

Figure 2d): Fatigue striations in Nimonic 80A (x7000).

Compound Stresses and Brittle Fracture Analysis

The failure of American all-welded ships during World War II stimulated extensive research into brittle fracture causes in steel. In standard tensile testing, plastic deformation involves shearing slip along crystal planes within crystals. However, when tension of equal magnitude exists in each principal direction, shearing stresses become absent, plastic deformation is prevented, and brittle fracture occurs once the material's cohesive strength is exceeded.

Equal triaxial tension stresses rarely arise in practical applications, but triaxial tension superimposed on unidirectional tension commonly occurs. When the margin between cohesive strength and plastic yield strength remains small, brittle fracture may occur in materials ordinarily considered highly ductile. Compound stresses develop in welds within very thick plates and in tubes under internal pressure combined with axial tension.

This phenomenon is illustrated in Fig. 3 through cohesive stress-strain curves B, N, and F. When two curves intersect at point Y, brittle fracture occurs preceded by plastic deformation, which decreases as the cohesive strength curve becomes lower relative to the yield stress-strain curve.

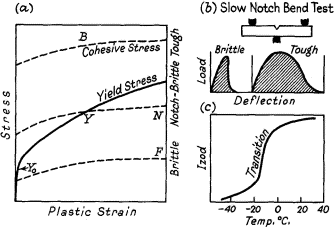
Figure 3: Cohesive stress-strain curves demonstrating the relationship between brittle fracture and plastic deformation

Material Brittleness Classification

Orowan demonstrated that when yield stress is denoted by Y, strength for brittle fracture by B (both Y and B depend on plastic strain), and the initial value of Y (for strain = 0) by Y₀, the following relationships apply:

The material exhibits brittleness if B < Y₀. The material demonstrates ductility but remains notch-brittle if Y₀ < B < 3Y₀. The material is not notch-brittle if 3Y < B.

The factor 3 accounts for stress increase at notch locations. Whether material exhibits notch-brittleness depends on the narrow margin between B and 3Y. Carbon steel represents an exceptional material because 3Y and B values are extremely close, explaining why Izod test results appear erratic and why notch brittleness shows high sensitivity to slight variations in composition, previous treatment, and temperature.

Brittle Fracture Characteristics and Crack Propagation

Brittle fracture is characterized by minimal work absorption and crystalline fracture surface appearance, often displaying chevron patterns pointing toward fracture origins. These patterns result from discontinuous cleavage crack formation and subsequent joining, as shown in Fig. 4. Brittle fracture can occur at relatively low stress levels of 75-120 MPa with remarkable suddenness. The velocity of crack propagation likely approaches the speed of sound in the material.

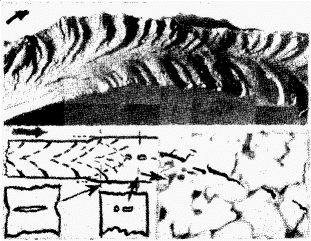
Figure 4: Steel brittle fracture surface with chevron markings, including a micrograph displaying discontinuous cracks ahead of the main crack

In this fracture type, plastic deformation remains very small, and cracks need not open considerably to propagate, unlike the requirements for ductile failure.

Griffith's Theory and Crack Propagation Energy

The work required for crack propagation follows Griffith's formula: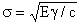

                  (1)

where σ represents tensile stress required to propagate a crack of length c, γ denotes surface energy of fracture faces, and E indicates Young's modulus.

Orowan modified Griffith's theory to include a plastic strain energy factor, ρ, since some plastic flow always occurs near fracture surfaces: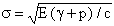

           (2)

When temperature exceeds the brittle-ductile transition temperature, ρ becomes large, and the stress σ required for crack growth also increases significantly. Below the transition temperature, the metal becomes brittle and ρ decreases. Consequently, the stress necessary for crack growth reduces substantially.

The reason for increasing crack propagation speed once cracking initiates becomes clear from both Griffith's and Orowan's equations: as crack length increases, the stress required for continued propagation continually decreases, creating a self-accelerating failure mechanism.

This comprehensive understanding of fracture mechanisms enables engineers to predict material behavior under various loading conditions and design more reliable structures that can withstand complex stress states while maintaining adequate safety margins.